Density Matrix Renormalization Group

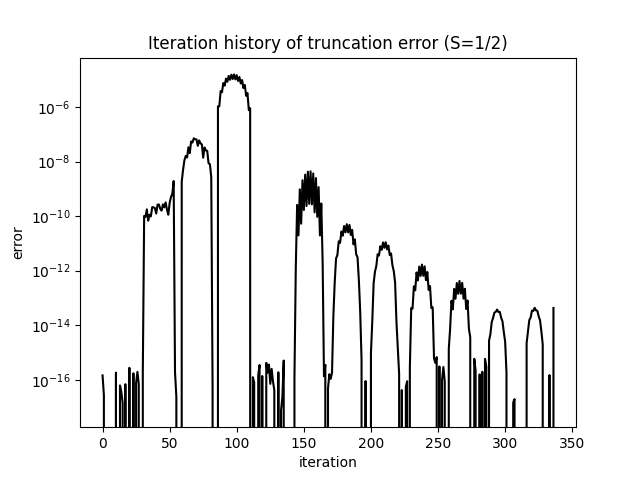
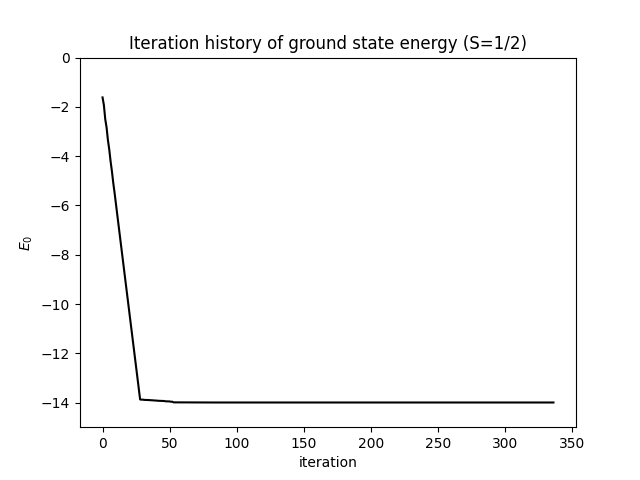
In this example, we will use Density Matrix Renormalization Group (DMRG) simulations to study the ground state energy of a 32-site spin-half Heisenberg chain with open boundary conditions. We will look at the convergence of the ground state energy as well as the decay of the truncation errors as functions of the iteration numbers.

We first import necessary libraries and set the parameters for the simulation.

import pyalps
import numpy as np
import matplotlib.pyplot as plt
import pyalps.plot

parms = [ { 
        'LATTICE'                   : "open chain lattice", 
        'MODEL'                     : "spin",
        'CONSERVED_QUANTUMNUMBERS'  : 'N,Sz',
        'Sz_total'                  : 0,
        'J'                         : 1,
        'SWEEPS'                    : 4,
        'NUMBER_EIGENVALUES'        : 1,
        'L'                         : 32,
        'MAXSTATES'                 : 100
       } ]

input_file = pyalps.writeInputFiles('parm_spin_one_half',parms)
res = pyalps.runApplication('dmrg',input_file,writexml=True)

To run this, in your computer terminal type

python spin_one_half.py

Next, we load the properties of the ground state measured by the DMRG code

data = pyalps.loadEigenstateMeasurements(pyalps.getResultFiles(prefix='parm_spin_one_half'))

and print them to the terminal.

for s in data[0]:
    print s.props['observable'], ' : ', s.y[0]

Additionally, we can load detailed data for each iteration step.

iter = pyalps.loadMeasurements(pyalps.getResultFiles(prefix='parm_spin_one_half'),
                          what=['Iteration Energy','Iteration Truncation Error'])

The above allows us to look at how the DMRG algorithm converged to the final results.

We finally plot the convergence of various quantities as functions of iterations.

plt.figure()
pyalps.plot.plot(iter[0][0])
plt.title('Iteration history of ground state energy (S=1/2)')
plt.ylim(-15,0)
plt.ylabel('$E_0$')
plt.xlabel('iteration')

plt.figure()
pyalps.plot.plot(iter[0][1])
plt.title('Iteration history of truncation error (S=1/2)')
plt.yscale('log')
plt.ylabel('error')
plt.xlabel('iteration')

plt.show()

The convergence of the ground state energy as a function of iteration numbers is shown in the following figure.

We can also take a look at the decay of the truncation error as the iteration number increases.

Exact Diagonaliztion