コンテンツにスキップ
Documentation
はじめに
DMRG

密度行列繰り込み群

このチュートリアルは pyalps がすでにインストールされていることを前提としています。まだセットアップしていない場合は、入門ガイドを参照してください。

DMRG とは？

**密度行列繰り込み群（DMRG）は Steven White によって 1992 年に提案され、1 次元量子格子モデルのデファクトスタンダードな手法となりました。DMRG は行列積状態（MPS）**の変分空間内で基底状態を探します。

∣ψ⟩=∑s1,…,sLA1s1A2s2⋯ALsL ∣s1s2⋯sL⟩, |\psi\rangle = \sum_{s_1, \ldots, s_L} A_1^{s_1} A_2^{s_2} \cdots A_L^{s_L} \, |s_1 s_2 \cdots s_L\rangle,

ここで各 AisiA_i^{s_i} は最大 m×mm \times m の行列です。整数 mm は**ボンド次元（bond dimension）**と呼ばれ、近似の精度を制御します。m=1m = 1 は積状態に対応し、mm を増やすことでより多くの量子もつれを記述できます。

なぜ 1 次元で非常に有効なのでしょうか。局所ハミルトニアンのギャップあり基底状態は面積則を満たします。任意の連続サイトブロックのもつれエントロピーは、ブロックサイズに依存しない定数で上界されます。これは、適度に固定された mm を持つ MPS で厳密な基底状態を十分に近似できることを意味します。S=1/2S = 1/2 ハイゼンベルク鎖（ギャップなし）ではもつれエントロピーが対数的にしか増大しないため、m∼100m \sim 100–10001000 で通常は十分です。

DMRG はスイープによって行列 AiA_i を最適化します。鎖の一端から始め、他のすべての行列を固定したまま各サイトの行列を順番に最適化し、もう一端からスイープバックする操作を収束するまで繰り返します。各最適化ステップは小さな固有値問題であり、ED が必要とする完全対角化よりはるかに安価です。DMRG スイープのコストは O(Lm3d)O(L m^3 d)（dd は局所ヒルベルト空間次元）であるのに対し、ED は O(dL)O(d^L) です。L=32L = 32、d=2d = 2 の場合、ED は約 232≈432^{32} \approx 43 億状態の処理が必要ですが、m=100m = 100 の DMRG は完全に実行可能です。

なぜ開放境界条件なのか？ DMRG は周期境界条件（PBC）よりも開放境界条件（OBC）の鎖に対してはるかに効率的です。PBC ではもつれ構造が鎖を一周するため、同じ精度を達成するためには実効的なボンド次元がほぼ 2 倍必要になります。そのため OBC が DMRG 計算の標準的な選択です。

物理モデル

L=32L = 32 サイト、開放境界条件の S=1/2S = 1/2 反強磁性ハイゼンベルク鎖を研究します。

H=J∑i=1L−1Si⋅Si+1,J>0. H = J \sum_{i=1}^{L-1} \mathbf{S}_i \cdot \mathbf{S}_{i+1}, \quad J > 0.

S=1S = 1 鎖（ハルデンギャップを持つ）と異なり、S=1/2S = 1/2 鎖はギャップなしです。その低エネルギースペクトルは冪乗則相関を持つ Tomonaga-Luttinger 液体（TLL）を形成します。熱力学的極限における結合あたりの厳密な基底状態エネルギーはベーテ仮説から得られます。

e0=14−ln⁡2≈−0.4431 J（結合あたり）. e_0 = \frac{1}{4} - \ln 2 \approx -0.4431\,J \quad \text{（結合あたり）}.

これは計算量子物理学で最もよく研究されているベンチマーク系の一つであり、DMRG を学ぶための理想的な出発点です。

シミュレーションの実行

設定、実行、解析のすべてを 1 つの Python スクリプトで行えます。

import pyalps
import numpy as np
import matplotlib.pyplot as plt
import pyalps.plot

parms = [ {
        'LATTICE'                  : "open chain lattice",   # 開放境界条件（DMRG に適している）
        'MODEL'                    : "spin",
        'CONSERVED_QUANTUMNUMBERS' : 'N,Sz',                 # N と Sz の保存を利用してブロック対角化
        'Sz_total'                 : 0,                      # Sz=0 セクターを対象（基底状態）
        'J'                        : 1,                      # 反強磁性交換
        'SWEEPS'                   : 4,                      # DMRG スイープ回数（左→右→左 = 1 スイープ）
        'NUMBER_EIGENVALUES'       : 1,                      # 基底状態のみを求める
        'L'                        : 32,                     # 鎖長
        'MAXSTATES'                : 100                     # ボンド次元 m（主要な精度パラメータ）
       } ]

input_file = pyalps.writeInputFiles('parm_spin_one_half', parms)
res = pyalps.runApplication('dmrg', input_file, writexml=True)

パラメータの説明

  • MAXSTATES は最も重要な精度パラメータで、最大ボンド次元 mm を設定します。mm を増やすと精度が向上しますが、計算時間は m3m^3 でスケールします。この 32 サイトベンチマークでは、m=100m = 100 で切断誤差を 10−610^{-6} 以下に抑えられます。
  • SWEEPS は完全なスイープ回数（左から右、そして戻る）です。ここでは 4 回で収束を示すのに十分ですが、本番計算では 10–20 回、またはスイープあたりのエネルギー変化が閾値を下回るまで繰り返すことが多いです。
  • CONSERVED_QUANTUMNUMBERS: 'N,Sz' は、全粒子数 NN と全磁化 SzS_z を良い量子数として利用し、MPS 行列をブロック対角化するよう DMRG に指示します。これにより計算が高速化され、数値的安定性も向上します。
  • NUMBER_EIGENVALUES: 1 は基底状態のみを対象とします。この値を増やすと、最低の複数の固有状態を同時に対象にできますが、追加コストがかかります。

基底状態の物理量の読み込み

シミュレーション後、loadEigenstateMeasurements は DMRG コードが測定したすべての物理量——エネルギー、磁化、相関関数、その他 ALPS が最終収束基底状態について計算した物理量——を取得します。

data = pyalps.loadEigenstateMeasurements(pyalps.getResultFiles(prefix='parm_spin_one_half'))

for s in data[0]:
    print(s.props['observable'], ' : ', s.y[0])

data[0] の各要素 s は 1 つの物理量に対応します。s.props['observable'] はその名前（例：'Energy'、'Magnetization'）で、s.y[0] はその値です。この 32 サイト開放鎖では、基底状態エネルギーは E0≈−14.3 JE_0 \approx -14.3\,J に近い値になるはずです。

反復履歴の読み込み

アルゴリズムの収束を確認するため、スイープごとの測定データを読み込みます。

itr = pyalps.loadMeasurements(pyalps.getResultFiles(prefix='parm_spin_one_half'),
                               what=['Iteration Energy', 'Iteration Truncation Error'])

itr[0][0] は各ハーフスイープで記録されたエネルギーを、itr[0][1] は各ステップの切断誤差を含みます。切断誤差は縮約密度行列の棄却固有値の和であり、mm 状態の MPS が表現できない厳密基底状態の重みを表します。よく収束した計算では切断誤差が 10−610^{-6} 以下になるべきです。このシステムの m=100m = 100 では、10−810^{-8}–10−710^{-7} 程度の値が典型的です。

収束のプロット 

plt.figure()
pyalps.plot.plot(itr[0][0])
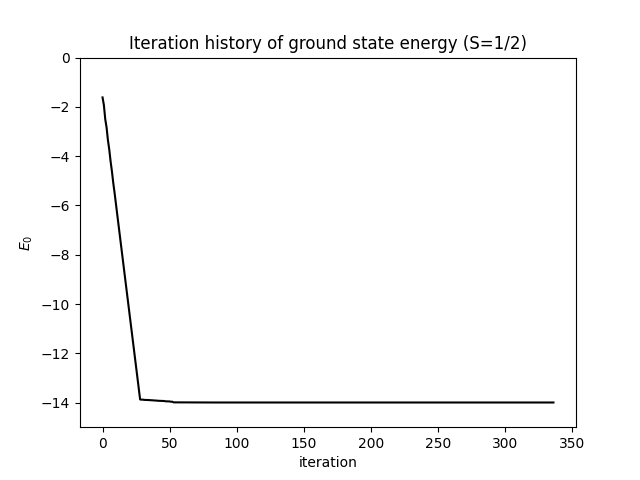
plt.title('Iteration history of ground state energy (S=1/2)')
plt.ylim(-15, 0)
plt.ylabel('$E_0$')
plt.xlabel('Iteration')

plt.figure()
pyalps.plot.plot(itr[0][1])
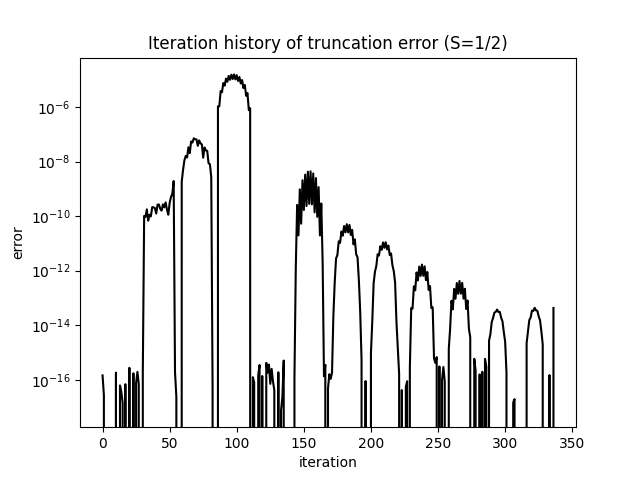
plt.title('Iteration history of truncation error (S=1/2)')
plt.yscale('log')
plt.ylabel('Truncation error')
plt.xlabel('Iteration')

plt.show()

結果

エネルギーは最初の数スイープで急速にプラトーへ収束します。以下の図はエネルギーの反復数依存性を示しており、最終スイープの前に安定しています。

DMRG 反復におけるエネルギー収束

切断誤差は対数スケールで単調に減少し、各スイープで MPS 近似の質が向上していることを反映しています。

DMRG 反復における切断誤差の減少（対数スケール）

両方の曲線が平坦になったら、計算は収束しています。精度をさらに向上させるには、MAXSTATES を増やし、エネルギーと切断誤差の変化が無視できることを確認してください。

CT-HYB厳密対角化法