厳密対角化法
疎行列厳密対角化法の例として、スピンチェーンモデルにおける三重項ギャップのシステムサイズ依存性を求めます。
まず、必要なパッケージをインポートします。
import pyalps
import numpy as np
import matplotlib.pyplot as plt
import pyalps.plot
import pyalps.fit_wrapper as fw次に入力パラメータを準備し、ALPSが期待する形式に書き込みます。
parms = []
for l in [4, 6, 8, 10, 12, 14, 16]:
for sz in [0, 1]:
parms.append(
{
'LATTICE' : "chain lattice", # チェーン格子
'MODEL' : "spin", # スピンモデル
'local_S' : 1, # 局所スピン
'J' : 1, # 交換相互作用
'L' : l, # システムサイズ
'CONSERVED_QUANTUMNUMBERS' : 'Sz', # 保存量
'Sz_total' : sz # 全スピンz成分
}
)
# 入力ファイルを書き出し
input_file = pyalps.writeInputFiles('parm2a',parms)各パラメータセットに対してsparsediagを実行します:
res = pyalps.runApplication('sparsediag',input_file)すべての状態の測定値を読み込みます:
data = pyalps.loadSpectra(pyalps.getResultFiles(prefix='parm2a'))各シミュレーションについて、全運動量における基底状態エネルギーを抽出します。
lengths = []
min_energies = {}
for sim in data:
l = int(sim[0].props['L'])
if l not in lengths: lengths.append(l)
sz = int(sim[0].props['Sz_total'])
all_energies = []
for sec in sim:
all_energies += list(sec.y)
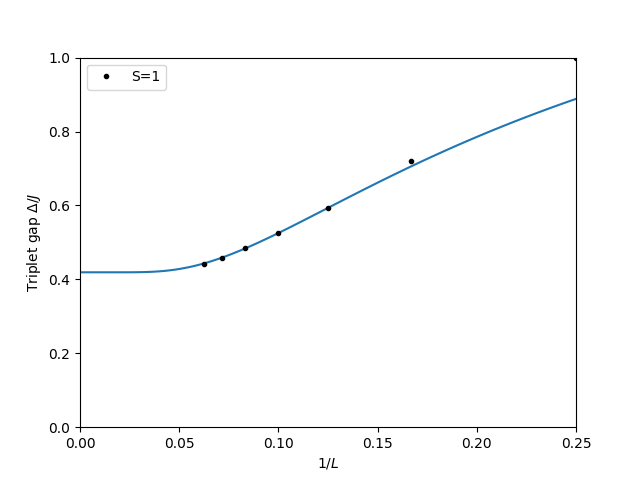
min_energies[(l,sz)]= np.min(all_energies)最後に、システムサイズに対する三重項ギャップのプロットを作成します。
gapplot = pyalps.DataSet()
gapplot.x = 1./np.sort(lengths)
gapplot.y = [min_energies[(l,1)] -min_energies[(l,0)] for l in np.sort(lengths)]
gapplot.props['xlabel']='$1/L$'
gapplot.props['ylabel']='三重項ギャップ $\Delta/J$'
gapplot.props['label']='S=1'
gapplot.props['line']='.'
plt.figure()
pyalps.plot.plot(gapplot)
plt.legend()
plt.xlim(0,0.25)
plt.ylim(0,1.0)
pars = [fw.Parameter(0.411), fw.Parameter(1000), fw.Parameter(1)]
f = lambda self, x, p: p[0]()+p[1]()*np.exp(-x/p[2]())
# L=8から16の範囲でフィッティング
fw.fit(None, f, pars, np.array(gapplot.y)[2:], np.sort(lengths)[2:])
x = np.linspace(0.0001, 1./min(lengths), 100)
plt.plot(x, f(None, 1/x, pars))
plt.show()最終結果は以下のようになります: