古典モンテカルロシミュレーション
古典モンテカルロ法の簡単な例として、2Dイジングモデルの相転移を求めます。
まず、必要なパッケージをインポートします。
import pyalps
import matplotlib.pyplot as plt
import pyalps.plot次に入力パラメータを準備します。ここではサイズ$4\times 4$、$8\times 8$、$16\times 16$の格子を異なる温度で考えます。
parms = []
for l in [4,8,16]:
for t in [5.0,4.5,4.0,3.5,3.0,2.9,2.8,2.7]:
parms.append(
{
'LATTICE' : "square lattice", # 正方格子
'T' : t, # 温度
'J' : 1 , # 交換相互作用
'THERMALIZATION' : 1000, # 熱化ステップ数
'SWEEPS' : 400000, # スイープ数
'UPDATE' : "cluster", # クラスター更新法
'MODEL' : "Ising", # イジングモデル
'L' : l # 格子サイズ
}
)
for t in [2.6, 2.5, 2.4, 2.3, 2.2, 2.1, 2.0, 1.9, 1.8, 1.7, 1.6, 1.5, 1.2]:
parms.append(
{
'LATTICE' : "square lattice",
'T' : t,
'J' : 1,
'THERMALIZATION' : 1000,
'SWEEPS' : 40000,
'UPDATE' : "cluster",
'MODEL' : "Ising",
'L' : l
}
)その後、Pythonを使用してALPSが期待する形式に入力を書き込み、入力ファイルを使ってスピンモンテカルロシミュレーション(spinmc)を実行するように指示します:
pyalps.evaluateSpinMC(pyalps.getResultFiles(prefix='parm7a'))
# 磁化率を読み込み、温度Tの関数として収集
data = pyalps.loadMeasurements(pyalps.getResultFiles(prefix='parm7a'),['|Magnetization|'])
magnetization_abs = pyalps.collectXY(data,x='T',y='|Magnetization|',foreach=['L'])
# プロット作成
plt.figure()
pyalps.plot.plot(magnetization_abs)
plt.xlabel('温度 $T$')
plt.ylabel('磁化 $|m|$')
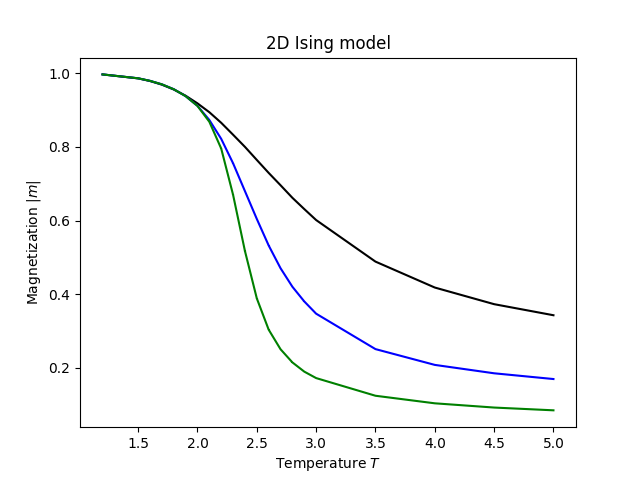
plt.title('2D イジングモデル')
plt.show()2Dイジングモデルの磁化について、以下の図が得られるはずです: