量子モンテカルロシミュレーション
量子モンテカルロシミュレーションの例として、半楕円形状態密度をハイブリダイゼーション関数として用いた、近藤効果による不純物の有効局在モーメントの温度低下シミュレーションを示します。
まず、必要なPythonモジュールをインポートします:
from pyalps.hdf5 import archive # hdf5インターフェース
import pyalps.cthyb as cthyb # ソルバーモジュール
import matplotlib.pyplot as plt # プロット用
from numpy import exp,log,sqrt,pi # 数学関数次に、対数スケールで等間隔な$0.05$から$100.0$までの$10$個の温度系列を生成します:
N_T = 10 # 温度点数
Tmin = 0.05 # 最低温度
Tmax = 100.0 # 最高温度
Tdiv = exp(log(Tmax/Tmin)/N_T)
T=Tmax
Tvalues=[]
for i in range(N_T+1):
Tvalues.append(T)
T/=Tdivサイト上の相互作用値、時間点数、各シミュレーションの時間制限を設定します:
Uvalues=[0.,2.] # サイト上相互作用の値
N_TAU = 1000 # タウ点数(最低温度に対して十分大きく設定)
runtime = 5 # ソルバーの実行時間(秒)シミュレーションパラメータを設定します:
values=[[] for u in Uvalues]
errors=[[] for u in Uvalues]
parameters=[]
for un,u in enumerate(Uvalues):
for t in Tvalues:
# 入力パラメータを準備
parameters.append(
{
# ソルバーパラメータ
'SWEEPS' : 1000000000, # 実行スイープ数
'THERMALIZATION' : 1000, # 熱化スイープ数
'SEED' : 42, # 乱数シード
'N_MEAS' : 10, # 測定間隔スイープ数
'N_ORBITALS' : 2, # 軌道数(スピン軌道自由度)
'BASENAME' : "hyb.param_U%.1f_BETA%.3f"%(u,1/t), # 出力ファイルベース名
'MAX_TIME' : runtime, # 反復あたりの実行時間
'VERBOSE' : 1, # 詳細出力
'TEXT_OUTPUT' : 0, # テキスト出力無効化
# ファイル名
'DELTA' : "Delta_BETA%.3f.h5"%(1/t), # ハイブリダイゼーション関数ファイル
'DELTA_IN_HDF5' : 1, # h5アーカイブからハイブリダイゼーションを読み込み
# 物理パラメータ
'U' : u, # ハバード斥力
'MU' : u/2., # 化学ポテンシャル
'BETA' : 1/t, # 逆温度
# 測定
'MEASURE_nnw' : 1, # 密度-密度相関関数(松原周波数)測定
'MEASURE_time' : 0, # 虚時間測定無効化
# 測定パラメータ
'N_HISTOGRAM_ORDERS' : 50, # 摂動次数ヒストグラムの最大次数
'N_TAU' : N_TAU, # 虚時間点数
'N_MATSUBARA' : int(N_TAU/(2*pi)), # 松原周波数点数
'N_W' : 1, # 局所磁化率のボゾン松原周波数点数
# 追加パラメータ
't' : 1, # ホッピング
'Un' : un, # 相互作用インデックス
}
)各パラメータセットに対して、ハイブリダイゼーション関数を設定します:
for parms in parameters:
ar=archive(parms['BASENAME']+'.out.h5','a')
ar['/parameters']=parms
del ar
print("ハイブリダイゼーション関数の初期化中...")
g=[]
I=complex(0.,1.)
mu=0.0
for n in range(parms['N_MATSUBARA']):
w=(2*n+1)*pi/parms['BETA']
g.append(2.0/(I*w+mu+I*sqrt(4*parms['t']**2-(I*w+mu)**2))) # 半楕円形状態密度のグリーン関数
delta=[]
for i in range(parms['N_TAU']+1):
tau=i*parms['BETA']/parms['N_TAU']
g0tau=0.0;
for n in range(parms['N_MATSUBARA']):
iw=complex(0.0,(2*n+1)*pi/parms['BETA'])
g0tau+=((g[n]-1.0/iw)*exp(-iw*tau)).real # テールを差し引いたフーリエ変換
g0tau *= 2.0/parms['BETA']
g0tau += -1.0/2.0 # テールの寄与を追加
delta.append(parms['t']**2*g0tau) # delta=t**2 g
# ハイブリダイゼーション関数をhdf5アーカイブに書き込み
ar=archive(parms['DELTA'],'w')
for m in range(parms['N_ORBITALS']):
ar['/Delta_%i'%m]=delta
del ar最後に、各パラメータセットに対してモンテカルロシミュレーションを実行します:
for parms in parameters:
# 不純物モデルを並列で解く
cthyb.solve(parms)シミュレーション終了後、各パラメータセットの結果を取得し、後処理してプロットします:
for parms in parameters:
# 局所スピン感受性を抽出
ar=archive(parms['BASENAME']+'.out.h5','w')
nn_0_0=ar['simulation/results/nnw_re_0_0/mean/value']
nn_1_1=ar['simulation/results/nnw_re_1_1/mean/value']
nn_1_0=ar['simulation/results/nnw_re_1_0/mean/value']
dnn_0_0=ar['simulation/results/nnw_re_0_0/mean/error']
dnn_1_1=ar['simulation/results/nnw_re_1_1/mean/error']
dnn_1_0=ar['simulation/results/nnw_re_1_0/mean/error']
nn = nn_0_0 + nn_1_1 - 2*nn_1_0
dnn = sqrt(dnn_0_0**2 + dnn_1_1**2 + ((2*dnn_1_0)**2) )
ar['chi']=nn/4.
ar['dchi']=dnn/4.
del ar
T=1/parms['BETA']
values[parms['Un']].append(T*nn[0])
errors[parms['Un']].append(T*dnn[0])
plt.figure()
plt.xlabel(r'$T$')
plt.ylabel(r'$4T\chi_{dd}$')
plt.title('不純物の近藤スクリーニング\n(ハイブリダイゼーション展開不純物ソルバー使用)')
for un in range(len(Uvalues)):
plt.errorbar(Tvalues, values[un], yerr=errors[un], label="U=%.1f"%Uvalues[un])
plt.xscale('log')
plt.legend()
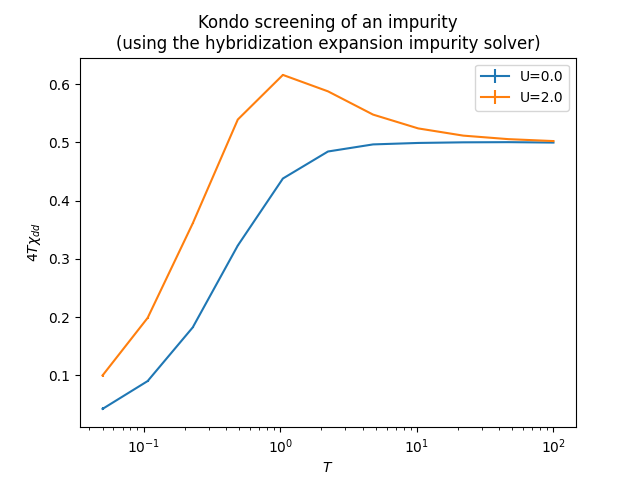
plt.show()この後、以下のプロットが得られます: