school
Monte Carlo Simulations
MC-02 Susceptibilities

MC-02 Susceptibilities

In this tutorial we will learn to calculate susceptibilities for classical and quantum Heisenberg models and contrast the behavior of chains and ladders as well as classical and quantum models.

Susceptibility of classical one-dimensional Heisenberg models

The one-dimensional Heisenberg classical chain

Preparing and running the simulation from the command line

The following parameters, downloadable here as parm2a, set up Monte Carlo simulations of the classical Heisenberg model on a one-dimensional chain with 60 sites for $T=0.05, 0.1, 0.2, \dots, 1.5$ using cluster updates:

LATTICE="chain lattice"
L=60
J=-1
THERMALIZATION=15000
SWEEPS=500000 
UPDATE="cluster" 
MODEL="Heisenberg"
{T=0.05;}
{T=0.1;}
{T=0.2;}
{T=0.3;}
{T=0.4;}
{T=0.5;}
{T=0.6;}
{T=0.7;}
{T=0.8;}
{T=0.9;}
{T=1.0;}
{T=1.25;}
{T=1.5;}

We run the simulation by using the standard sequence of commands:

parameter2xml parm2a
spinmc --Tmin 10 --write-xml parm2a.in.xml

To extract the results, we recommend the Python evaluation tools discussed below.

Preparing and running the simulation using Python

The script we use, tutorial2a.py, is downloadable here. We recommend placing it in the same folder as parm2a. In this script we first import the required modules and then prepare the input parameters as a list of Python dictionaries:

import pyalps
import matplotlib.pyplot as plt
import pyalps.plot
parms = []
for t in [0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.25, 1.5, 1.75, 2.0]:
parms.append(
    { 
        'LATTICE'        : "chain lattice", 
        'T'              : t,
        'J'              : -1 ,
        'THERMALIZATION' : 10000,
        'SWEEPS'         : 500000,
        'UPDATE'         : "cluster",
        'MODEL'          : "Heisenberg",
        'L'              : 60
    }
)

We next convert this into a job file in XML format and run the simulation:

input_file = pyalps.writeInputFiles('parm2a',parms)
pyalps.runApplication('spinmc',input_file,Tmin=5,writexml=True)

We now have the same output files as in the command line version.

Evaluating the simulation and preparing plots using Python

To prepare plots, we load the results from the output files for this simulation (so, the output files starting with parm2a) and collect the susceptibility as a function of temperature. We do this in the same script in which we ran the simulation, but if you want to view the results again without redoing the simulation, you may also create a new script, named something like loader2a.py. If you do the latter, you must once again import necessary modules.

import pyalps
import matplotlib.pyplot as plt
import pyalps.plot

The code to load the results is

data = pyalps.loadMeasurements(pyalps.getResultFiles(prefix='parm2a'),'Susceptibility')

and to collect susceptibility as a function of temperature we write

susceptibility = pyalps.collectXY(data,x='T',y='Susceptibility')

To plot this data, we create a new matplotlib figure, call pyalps.plot.plot on the object created when we collected the susceptibility, and then set some nice labels, a title, and a range of y-values:

plt.figure()
pyalps.plot.plot(susceptibility)
plt.xlabel('Temperature $T/J$')
plt.ylabel('Susceptibility $\chi J$')
plt.ylim(0,0.22)
plt.title('Classical Heisenberg chain')
plt.show()

The one-dimensional classical Heisenberg ladder

The Heisenberg ladder is simulated in a very similar way. The main differences (besides naming the files parm2b*) is a change of the LATTICE and the presence of two couplings: J0 for the sides, and J1 for the rungs.

To set up and run the simulation on the command line, we first use a parameter file parm2b, placed in the same folder as parm2a:

LATTICE="ladder"
L=60
J0=-1
J1=-1
THERMALIZATION=15000
SWEEPS=150000
UPDATE="cluster"
MODEL="Heisenberg"
...

The rest of the parameter file is as in the chain case and the simulations are run in the same way.

To set up and run the simulation in Python we create a copy of tutorial2a.py named tutorial2b.py in the same folder, or we may download it here. We make the following changes:

  • renaming parm2a to parm2b
  • changing the parameter LATTICE to "ladder"
  • setting two couplings J0 and J1

Questions

  • How does the susceptibility depend on the lattice shape? What is the difference in susceptibility for a chain and a ladder?
  • Bonus: You can study larger system sizes and different types of lattices (“cubic lattice”, “triangular lattice”, check the file lattices.xml), as well.

Susceptibility of one-dimensional quantum Heisenberg models

The one-dimensional quantum Heisenberg chain

The main differences for simulating quantum models are that we use the ALPS model library to specify the model, and the ALPS looper QMC code to run the simulations. Note also that in quantum models there is usually a different sign convention for the couplings: positive couplings refer to the antiferromagnetic case.

Preparing and running the simulation from the command line

To set up and run the simulation on the command line we first download the parameter file parm2c and place it in the same folder:

LATTICE=“chain lattice” MODEL=“spin” local_S=1/2 L=60 J=1 THERMALIZATION=15000 SWEEPS=150000 ALGORITHM=“loop” {T=0.05;} {T=0.1;} {T=0.2;} {T=0.3;} {T=0.4;} {T=0.5;} {T=0.6;} {T=0.7;} {T=0.75;} {T=0.8;} {T=0.9;} {T=1.0;} {T=1.25;} {T=1.5;} {T=1.75;} {T=2.0;}

The looper code requires an additional ALGORITHM parameter to choose the algorithm and representation. The simulation is then run by running:

parameter2xml parm3a
loop parm3a.in.xml

Preparing and running the simulation using Python

To set up and run the simulation in Python we create another copy of tutorial2a.py in the same folder, and name it tutorial2c.py. We simply change the parameters to those described for parm2c, and the filename to parm2c. The altered script may be downloaded here.

input_file = pyalps.writeInputFiles('parm2c',parms)
pyalps.runApplication('loop',input_file)

The one-dimensional quantum Heisenberg ladder

Finally, we can look at a quantum Heisenberg ladder. By now you should be able to run simulations from either the command line or Python just from input parameters.

The filename for this case shall be parm2d. We set two couplings, J0 and J1, both to +1, but aside from changing LATTICE to "ladder" there are no other changes to the parameters. tutorial2d.py may be downloaded here.

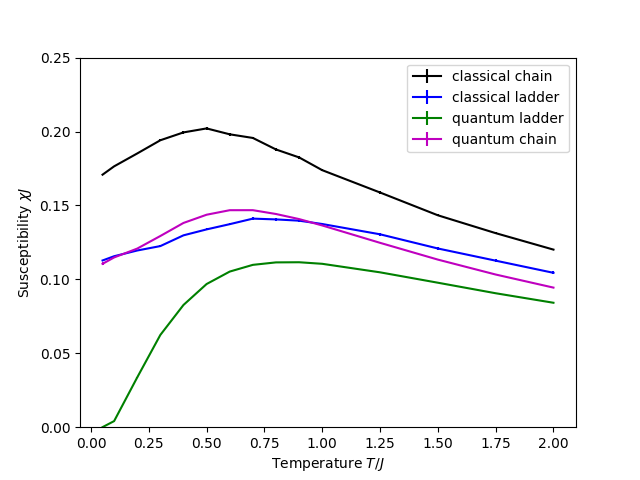
Combining all simulations

We want to plot the magnetic susceptibility against the temperature for all four previous simulations on the same plot. To do this, we use Python.

Using Python

After running all four simulations in the same folder, we may run the script tutorial2full.py in that folder. First, we load all susceptibility results with pyalps.loadMeasurements and pyalps.getResultFiles, and use pyalps.flatten to flatten results from different files into one data structure containing data from all simulations:

import pyalps
import matplotlib.pyplot as plt
import pyalps.plot

data = pyalps.loadMeasurements(pyalps.getResultFiles(),'Susceptibility')
data = pyalps.flatten(data)

Note that pyalps.getResultFiles, when run with no parameters, searches for all output files within the folder of the script. Also note that pyalps.flatten preserves the parameters from which each set of results was obtained, and all it does is make it as if those results were all present in a single file, rather than spread out across multiple.

We use pyalps.collectXY to collect the susceptibility as a function of temperature, and use the foreach parameter to sort this data into a different set for each value of the LATTICE and MODEL parameters:

susceptibility = pyalps.collectXY(data,x='T',y='Susceptibility',foreach=['MODEL','LATTICE'])

Next, we query each dataset for its LATTICE and MODEL parameters to set its label to something sensible (these labels will be used to generate a legend for the plot):

for s in susceptibility:
if s.props['LATTICE']=='chain lattice':
    s.props['label'] = "chain"
elif s.props['LATTICE']=='ladder':
    s.props['label'] = "ladder"
if s.props['MODEL']=='spin':
    s.props['label'] = "quantum " + s.props['label']
elif s.props['MODEL']=='Heisenberg':
    s.props['label'] = "classical " + s.props['label']

We may finally plot the data.

plt.figure()
pyalps.plot.plot(susceptibility)
plt.xlabel('Temperature $T/J$')
plt.ylabel('Susceptibility $\chi J$')
plt.ylim(0,0.25)
plt.legend()
plt.show()

Questions

  • Is there a difference between the classical and quantum calculation?
  • How does the susceptibility depend on the lattice? What is the difference between a chain lattice and a ladder?
  • Why does the susceptibility change with temperature?

For your reference, here is a plot created by the last workflow which combines all four calculations:

Contributors

  • Simon Trebst
  • Fabien Alet
  • Matthias Troyer
  • Synge Todo
  • Emanuel Gull
  • Abdullah “Amina” Al-Harbi
MC-01b EquilibrationMC-03 Magnetization