密度矩阵重整化群

在这个例子中，我们将使用密度矩阵重整化群（DMRG）模拟来研究具有开边界条件的 32 格点自旋半整数海森堡链的基态能量。我们将观察基态能量的收敛性以及截断误差作为迭代次数函数的衰减。

我们首先导入必要的库并设置模拟参数。

import pyalps
import numpy as np
import matplotlib.pyplot as plt
import pyalps.plot

parms = [ { 
        'LATTICE'                   : "open chain lattice", 
        'MODEL'                     : "spin",
        'CONSERVED_QUANTUMNUMBERS'  : 'N,Sz',
        'Sz_total'                  : 0,
        'J'                         : 1,
        'SWEEPS'                    : 4,
        'NUMBER_EIGENVALUES'        : 1,
        'L'                         : 32,
        'MAXSTATES'                 : 100
       } ]

input_file = pyalps.writeInputFiles('parm_spin_one_half',parms)
res = pyalps.runApplication('dmrg',input_file,writexml=True)

要运行此程序，在您的计算机终端中输入：

python spin_one_half.py

接下来，我们加载由 DMRG 代码测量的基态属性：

data = pyalps.loadEigenstateMeasurements(pyalps.getResultFiles(prefix='parm_spin_one_half'))

并将它们打印到终端。

for s in data[0]:
    print(s.props['observable'], ' : ', s.y[0])

此外，我们可以加载每个迭代步骤的详细数据。

iter = pyalps.loadMeasurements(pyalps.getResultFiles(prefix='parm_spin_one_half'),
                          what=['Iteration Energy','Iteration Truncation Error'])

上述代码允许我们观察 DMRG 算法如何收敛到最终结果。

最后，我们绘制各种量作为迭代次数函数的收敛图。

plt.figure()
pyalps.plot.plot(iter[0][0])
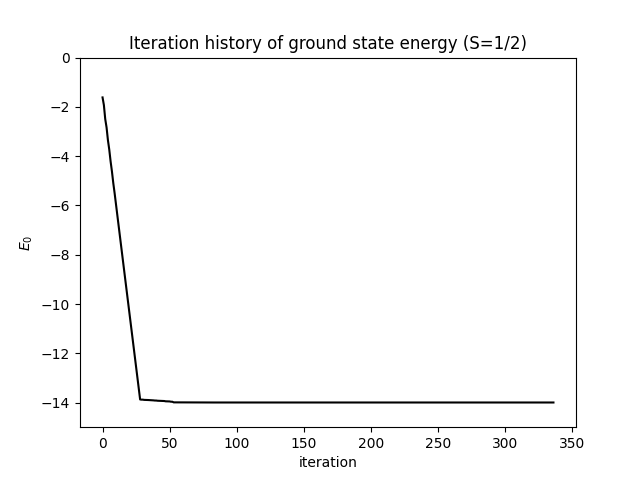
plt.title('Iteration history of ground state energy (S=1/2)')
plt.ylim(-15,0)
plt.ylabel('$E_0$')
plt.xlabel('iteration')

plt.figure()
pyalps.plot.plot(iter[0][1])
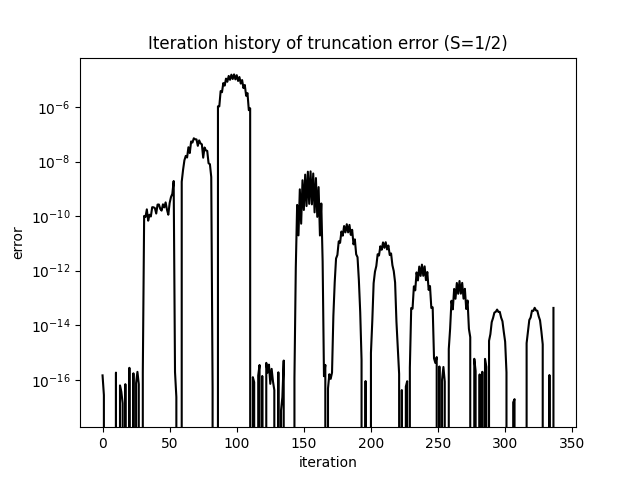
plt.title('Iteration history of truncation error (S=1/2)')
plt.yscale('log')
plt.ylabel('error')
plt.xlabel('iteration')

plt.show()

基态能量作为迭代次数函数的收敛性如下图所示。 Ground State Energy

我们还可以观察截断误差随迭代次数增加的衰减情况。 Truncation Error

精确对角化