经典蒙特卡洛模拟
作为经典蒙特卡洛的简单示例,我们考虑在二维伊辛模型中通过数值模拟来揭示其在低温下的相变。
首先,我们需要导入所需的包。
import pyalps
import matplotlib.pyplot as plt
import pyalps.plot然后我们准备输入参数。这里我们考虑不同温度下的 $4\times 4$、$8\times 8$、$16\times 16$ 尺寸的晶格。
parms = []
for l in [4,8,16]:
for t in [5.0,4.5,4.0,3.5,3.0,2.9,2.8,2.7]:
parms.append(
{
'LATTICE' : "square lattice",
'T' : t,
'J' : 1 ,
'THERMALIZATION' : 1000,
'SWEEPS' : 400000,
'UPDATE' : "cluster",
'MODEL' : "Ising",
'L' : l
}
)
for t in [2.6, 2.5, 2.4, 2.3, 2.2, 2.1, 2.0, 1.9, 1.8, 1.7, 1.6, 1.5, 1.2]:
parms.append(
{
'LATTICE' : "square lattice",
'T' : t,
'J' : 1,
'THERMALIZATION' : 1000,
'SWEEPS' : 40000,
'UPDATE' : "cluster",
'MODEL' : "Ising",
'L' : l
}
)之后,我们使用 Python 来输入 ALPS 预期的运行参数格式,并告诉它使用输入文件运行自旋蒙特卡洛模拟(spinmc):
#写入输入文件并运行模拟
input_file = pyalps.writeInputFiles('parm7a',parms)
pyalps.runApplication('spinmc',input_file,Tmin=5)模拟完成后,我们可以评估和绘制结果。
pyalps.evaluateSpinMC(pyalps.getResultFiles(prefix='parm7a'))
#加载磁化强度并将其作为温度 T 的函数收集
data = pyalps.loadMeasurements(pyalps.getResultFiles(prefix='parm7a'),['|Magnetization|'])
magnetization_abs = pyalps.collectXY(data,x='T',y='|Magnetization|',foreach=['L'])
#制作图表
plt.figure()
pyalps.plot.plot(magnetization_abs)
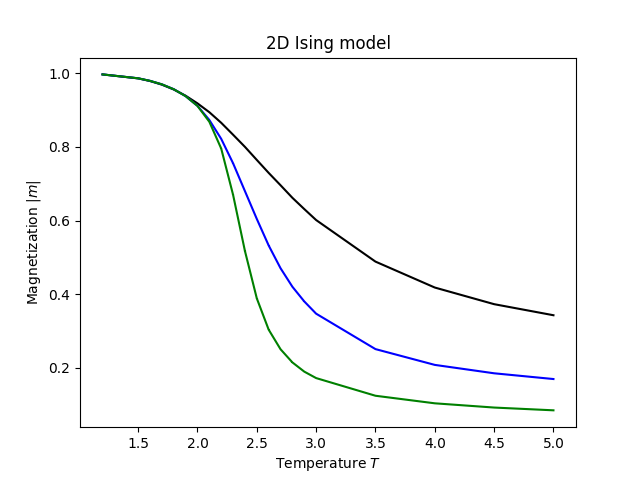
plt.xlabel('温度 $T$')
plt.ylabel('磁化强度 $|m|$')
plt.title('二维伊辛模型')
plt.show()我们应该得到以下二维伊辛模型磁化强度的图形: