量子蒙特卡洛模拟
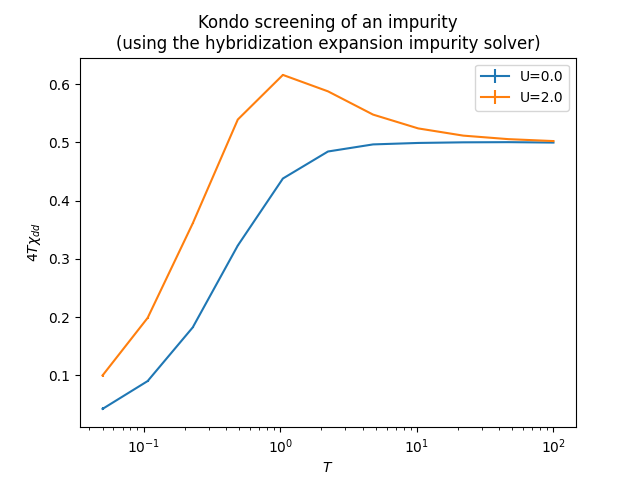
作为量子蒙特卡洛模拟的示例,我们展示了一个模拟杂质有效局域磁矩随温度降低而产生近藤屏蔽效应的仿真,使用半椭圆态密度作为杂化函数。
首先,我们导入所有必需的 python 模块:
from pyalps.hdf5 import archive # hdf5 接口
import pyalps.cthyb as cthyb # 求解器模块
import matplotlib.pyplot as plt # 用于绘制结果
from numpy import exp,log,sqrt,pi # 一些数学函数现在我们生成一个在 $0.05$ 和 $100.0$ 之间的 $10$ 个温度序列,这些温度在对数尺度上等距分布:
N_T = 10 # 温度数量
Tmin = 0.05 # 最高温度
Tmax = 100.0 # 最低温度
Tdiv = exp(log(Tmax/Tmin)/N_T)
T=Tmax
Tvalues=[]
for i in range(N_T+1):
Tvalues.append(T)
T/=Tdiv我们设置现场相互作用的值、时间点数量和每次模拟的时间限制:
Uvalues=[0.,2.] # 现场相互作用的值
N_TAU = 1000 # tau点数;对于最低温度必须足够大(至少设置为 5*BETA*U)
runtime = 5 # 求解器运行时间(秒)然后我们设置模拟参数:
values=[[] for u in Uvalues]
errors=[[] for u in Uvalues]
parameters=[]
for un,u in enumerate(Uvalues):
for t in Tvalues:
# 准备输入参数;它们可以在脚本内使用并传递给求解器
parameters.append(
{
# 求解器参数
'SWEEPS' : 1000000000, # 要执行的扫描次数
'THERMALIZATION' : 1000, # 要执行的热化扫描次数
'SEED' : 42, # 随机数种子
'N_MEAS' : 10, # 执行测量前的扫描次数
'N_ORBITALS' : 2, # "轨道"数量,即自旋轨道自由度或段的数量
'BASENAME' : "hyb.param_U%.1f_BETA%.3f"%(u,1/t), # h5 输出文件的基本名称
'MAX_TIME' : runtime, # 每次迭代的求解器运行时间
'VERBOSE' : 1, # 是否输出额外信息
'TEXT_OUTPUT' : 0, # 是否以人类可读(文本)格式写入结果
# 文件名
'DELTA' : "Delta_BETA%.3f.h5"%(1/t), # 杂化函数的文件名
'DELTA_IN_HDF5' : 1, # 是否从 h5 存档读取杂化
# 物理参数
'U' : u, # 哈伯德排斥
'MU' : u/2., # 化学势
'BETA' : 1/t, # 逆温度
# 测量
'MEASURE_nnw' : 1, # 测量松原频率上的密度-密度相关函数(局域磁化率)
'MEASURE_time' : 0, # 关闭虚时测量
# 测量参数
'N_HISTOGRAM_ORDERS' : 50, # 微扰阶数直方图的最大阶数
'N_TAU' : N_TAU, # 虚时点数(tau_0=0, tau_N_TAU=BETA)
'N_MATSUBARA' : int(N_TAU/(2*pi)), # 松原频率数量
'N_W' : 1, # 局域磁化率的玻色子松原频率数量
# 附加参数(仅在求解器外使用)
't' : 1, # 跳跃
'Un' : un, # 相互作用点
}
)对于每组参数,我们设置杂化函数:
for parms in parameters:
ar=archive(parms['BASENAME']+'.out.h5','a')
ar['/parameters']=parms
del ar
print("创建初始杂化...")
g=[]
I=complex(0.,1.)
mu=0.0
for n in range(parms['N_MATSUBARA']):
w=(2*n+1)*pi/parms['BETA']
g.append(2.0/(I*w+mu+I*sqrt(4*parms['t']**2-(I*w+mu)**2))) # 使用半椭圆态密度的格林函数
delta=[]
for i in range(parms['N_TAU']+1):
tau=i*parms['BETA']/parms['N_TAU']
g0tau=0.0;
for n in range(parms['N_MATSUBARA']):
iw=complex(0.0,(2*n+1)*pi/parms['BETA'])
g0tau+=((g[n]-1.0/iw)*exp(-iw*tau)).real # 减去尾部的傅里叶变换
g0tau *= 2.0/parms['BETA']
g0tau += -1.0/2.0 # 添加回尾部贡献
delta.append(parms['t']**2*g0tau) # delta=t**2 g
# 将杂化函数写入 hdf5 存档(求解器输入)
ar=archive(parms['DELTA'],'w')
for m in range(parms['N_ORBITALS']):
ar['/Delta_%i'%m]=delta
del ar最后,我们对每组参数运行蒙特卡洛模拟:
for parms in parameters:
# 并行求解杂质模型
cthyb.solve(parms)模拟完成后,我们获得每组参数的结果,对其进行后处理并绘制图表:
for parms in parameters:
# 提取局域自旋磁化率
ar=archive(parms['BASENAME']+'.out.h5','w')
nn_0_0=ar['simulation/results/nnw_re_0_0/mean/value']
nn_1_1=ar['simulation/results/nnw_re_1_1/mean/value']
nn_1_0=ar['simulation/results/nnw_re_1_0/mean/value']
dnn_0_0=ar['simulation/results/nnw_re_0_0/mean/error']
dnn_1_1=ar['simulation/results/nnw_re_1_1/mean/error']
dnn_1_0=ar['simulation/results/nnw_re_1_0/mean/error']
nn = nn_0_0 + nn_1_1 - 2*nn_1_0
dnn = sqrt(dnn_0_0**2 + dnn_1_1**2 + ((2*dnn_1_0)**2) )
ar['chi']=nn/4.
ar['dchi']=dnn/4.
del ar
T=1/parms['BETA']
values[parms['Un']].append(T*nn[0])
errors[parms['Un']].append(T*dnn[0])
plt.figure()
plt.xlabel(r'$T$')
plt.ylabel(r'$4T\chi_{dd}$')
plt.title('Kondo screening of an impurity\n(using the hybridization expansion impurity solver)')
for un in range(len(Uvalues)):
plt.errorbar(Tvalues, values[un], yerr=errors[un], label="U=%.1f"%Uvalues[un])
plt.xscale('log')
plt.legend()
plt.show()之后,您将得到以下图表: